Special Right Triangle 30 60 90 Triangle Sides

A right triangle with a 30 angle or 60 angle must be a 30 60 90 special right triangle. They are special because with simple geometry we can know the ratios of their sides. Enter 1 out of 3 to solve for the other 2 missing sides.

subiecte bac 2012 romana subiecte bac 2016 fizica subiecte bac 2017 istorie subiecte bac 2019 fizica subiecte admitere politehnica 2018 subiecte bac 2017 limba romana subiecte bac 2017 matematica m2 subiecte bac 2019 biologie

Special Right Triangles Fully Explained W 19 Examples

The Easy Guide To The 30 60 90 Triangle

How To Work With 30 60 90 Degree Triangles Education Is Around

30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com

The Complete Guide To The 30 60 90 Triangle

30 60 90 Right Triangles Read Geometry Ck 12 Foundation

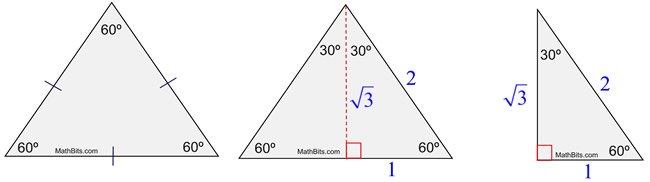
The fact that the remaining leg ad has length 3 follows immediately from the pythagorean theorem.

Special right triangle 30 60 90 triangle sides. Find the value of x. The other is the isosceles right triangle. Special right triangle 30 60 90 is one of the most popular right triangles. Isosceles and 30 60 90 video.

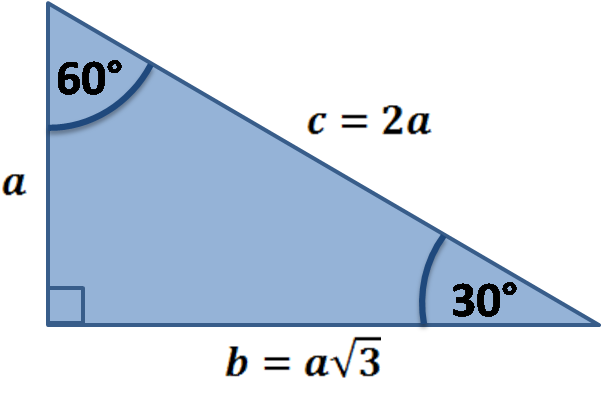
One is the 30 60 90 triangle. A 30 60 90 right triangle is a special right triangle in which one angle measures 30 degrees and the other 60 degrees. Its properties are so special because it s half of the equilateral triangle. There are two special triangles in trigonometry.

Which of the following are not the lengths of the sides of a 30 60 90 triangle. The key characteristic of a 30 60 90 right triangle is that its angles have measures of 30 degrees π 6 rads 60 degrees π 3 rads and 90 degrees π 2 rads. Start studying special right triangles quiz. A right triangle with a 30 angle or 60 angle must be a 30 60 90 special right triangle.

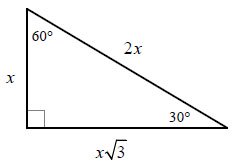
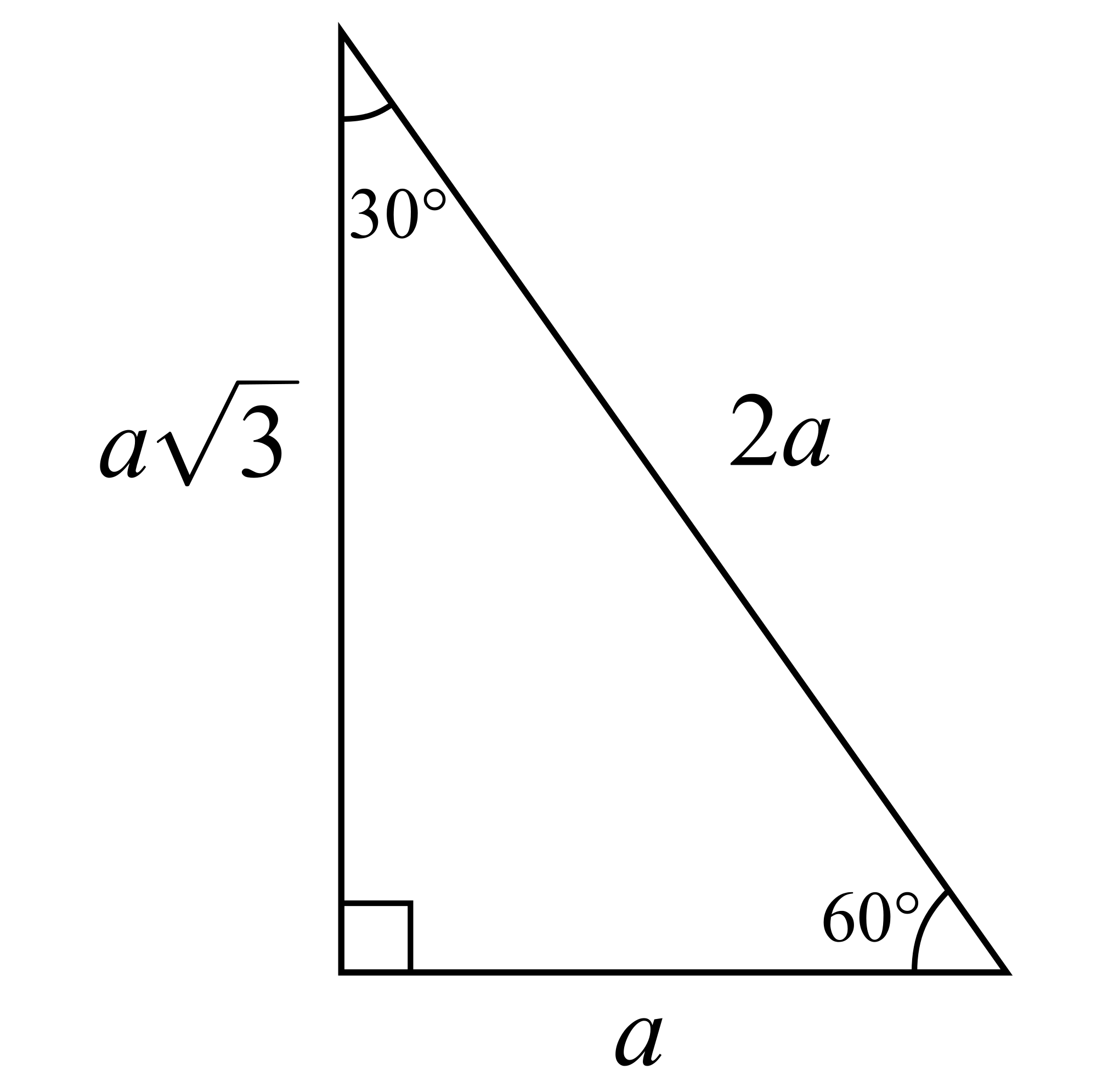
In a 30 60 90 triangle the sides are in the ratio 1. Special right triangles 30 60 90. Then abd is a 30 60 90 triangle with hypotenuse of length 2 and base bd of length 1. In a 30 60 90 triangle.

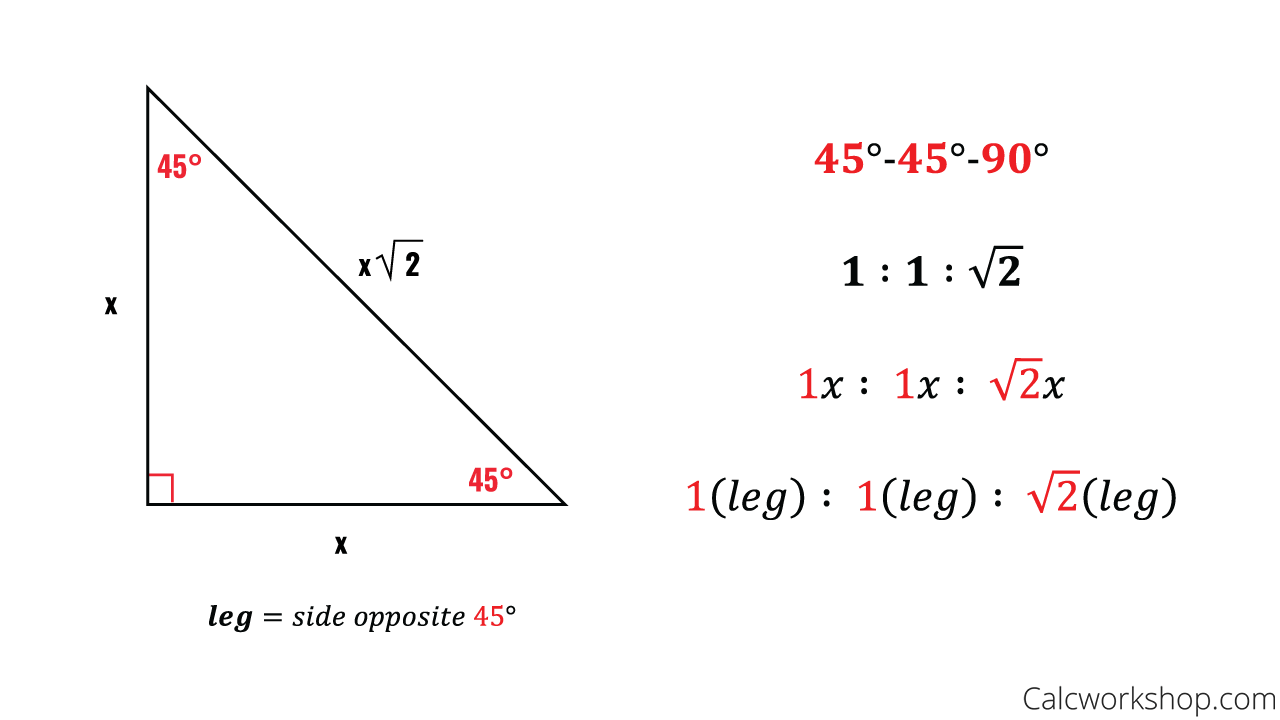
Find the length of the hypotenuse of a right triangle if the lengths of the other two sides are 4 inches and 4 dadic 3 inches. The 30 60 90 triangle is the only right triangle whose angles are in an arithmetic progression. Hypotenuse x. In a 45 45 90 triangle the length of the hypotenuse is 11.

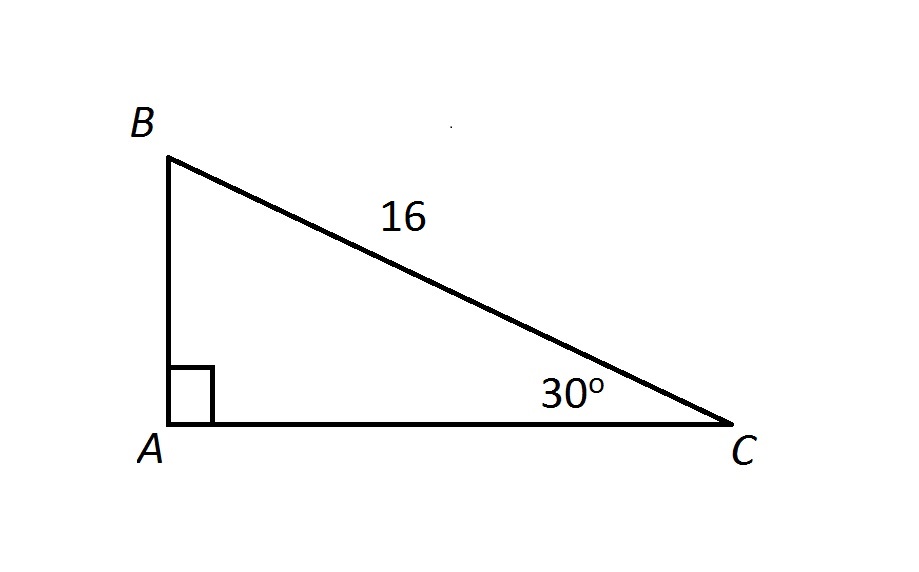
If you have one side you can use these formulas and maybe a little algebra to get the others. You are given that the hypotenuse is 8. If you want to read more about that special shape check our calculator dedicated to the 30 60 90 triangle. The sides of a 30 60 90 right triangle lie in the ratio 1 3 2.

Find the lengths of the other two sides of a right triangle if the length of the hypotenuse is 8 inches and one of the angles is 30. Learn vocabulary terms and more with flashcards. We will prove that below. In an isosceles right triangle the angle measures are 45 45 90 and the side lengths create a ratio where the measure of the hypotenuse is sqrt 2 times the measure of each leg as seen in the diagram below.

If you have one side you can use these formulas and maybe a little algebra to get the others. This is a right triangle with a 30 60 90 triangle. Isosceles and 30 60 90 video watch the special triangles.